

1.実験計画書
実験計画法による実験も信頼性試験も当初の目的を達成するには、綿密な実験計画書の作成が必須である。エンジニアが実施する実験は技術的な観点でのテーマが殆どで、その実施者とデータ解析者(評価者)も同一人物であることが多いことから、往々にしてメモ書き程度の実験計画書で実施されることもあるが、実験規模、要素技術レベルの度合いに関わらず実験計画書を作成することが推奨される。実験後の分析評価時点で設計情報の不足により設計Par.を決定できなかったということを管理人も幾度が経験しており、因子水準の設定を一つ誤るだけでも所要の設計情報が得られないことがある。よく言われることでありここで書くまでもないが、実験の成否は実験計画書の作成時点で決定すると言っても過言ではなく、下記の項目を検討し決定する過程で実験に潜む種々の問題を洗い出すことで、結果の信憑性、再現性を高められる。これらの項目は実験計画のプロセスそのものであり、更にこれらの項目を纏めておくことで分析(評価)結果を報告する際の技術報告書の作成も容易になる。
●実験計画書に記載する項目例
・目的(背景、経緯などの情報整理)
・因子水準表(因子の種類/水準の設定)
・実験(試験)条件
・実験試料(水準組み合わせ/試料数、サンプリング法など)
・測定項目(特性値の選定/測定方法)
・取得データの分析手法
・実験スケジュール
2.ANOVA1,2
2.1解析データ
ある電気機器の調整済特性値が、製造工程の進捗に伴い変化している可能性があることが分かった。工程間で差があるかを5水準の一元配置で検証するべく、各工程(A~E)から25個無作為にサンプリングし以下のデータを得た。分散分析表を作成し工程間で差があるかを検証せよ。なお特性値の検査規格は25±4で既知情報としての工程能力指数はCp≒1.2である
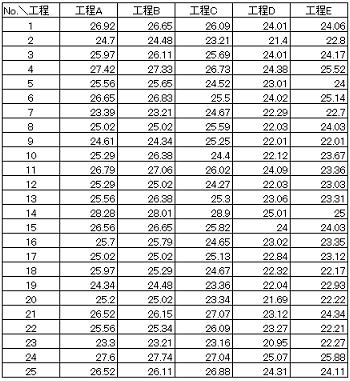
2.2分散分析表の作成
1)総平方和の計算
総平方和は以下の式のように展開整理すると計算が楽である。勿論最後の式に至る過程は省略されてはいるが、これに至る過程の証明は我々にとっては然程重要ではなく、このように計算すれば求められることが証明されているので、これに従って計算するだけである。
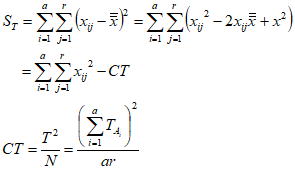
上の式の各項を求めるべく因子水準データから各因子水準の合計値と総合計、水準平均、合計値の二乗和を求めると以下のように計算される。
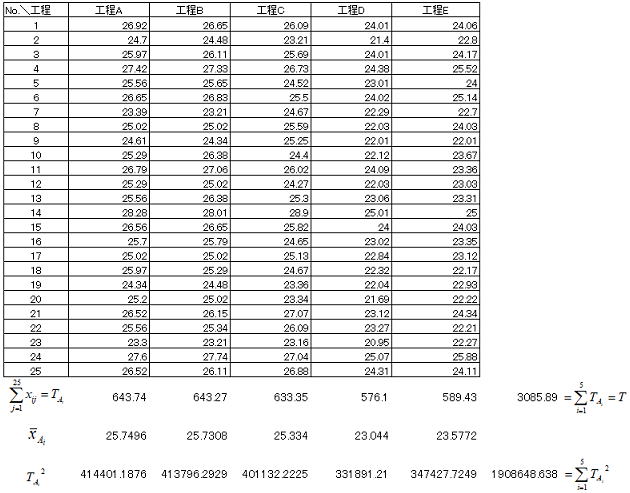
各因子水準のデータの二乗和からデータの総二乗和を求め、CT値を計算後総平方和(ばらつき)を計算する。
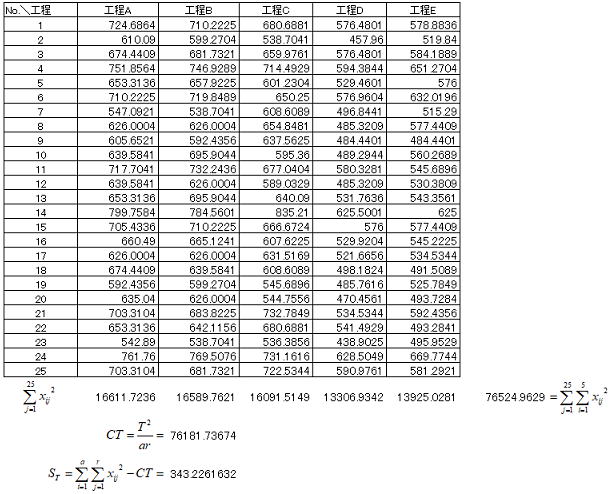
上記経験結果と以下の式より水準間(水準の違いに起因する)ばらつきを求め、ST-SAより誤差項Seが求まる。分散分析表ではこれらの値(各平方和)をそれぞれの自由度で割り不偏分散を求め、その分散比(F0)が自由度(φA,φe)のF分布に従うことを利用して、F(φA,φe,α)=F(4,120,0.05)≒2.45と比較し因子水準(工程)間に差があるかのF検定を行う。本分散分析ではF0>F(φA,φe,0.05)のため、製造工程の進捗に伴い電気機器の特性値は変化していると判断された。
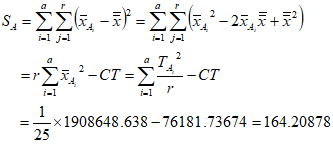

2)母平均の推定
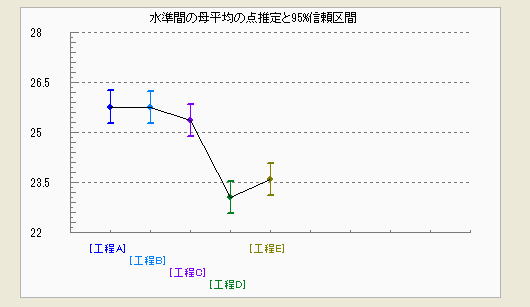
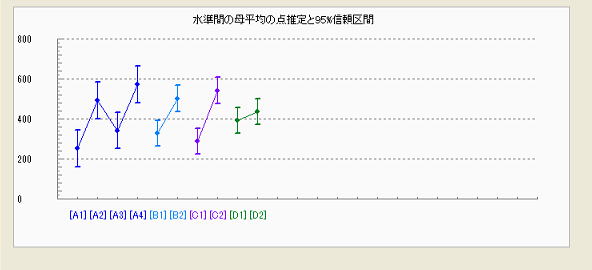
各水準の母平均の点推定値と母分散が未知の場合の推定理論より、以下の式により信頼率(1-α)の区間推定を行う。以下の表の計算結果によると、工程A~Cでは殆ど変化は認められないが工程C→工程Dに移った際に約2.3程度変化(低下)していることが分かった。3)項の母標準偏差の推定値がσ≒1.22なので平均が約1.9σ分低い側に移動したことになり、工程能力指数のCpk=(1-K)CpにおけるKの値は0.5程度になることから、この変化は無視できない値といえる。
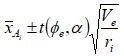

3)母標準偏差の推定
分散分析表における誤差分散はデータの構造式における誤差εの母分散の推定量となることから、母標準偏差の推定量は以下の式により得られσ≒1.22と推定された。設問より特性値の規格幅は8なので、この値から推定される工程能力指数はCp=(USL-LSL)/6σ=8/1.22×6=8/7.32≒1.1となり既知情報としてのCp≒1.2とほぼ同程度の値が得られており、この評価結果は信頼できるものといえる。
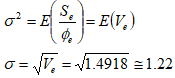
2.3プログラム(SA&RA ProX)による解析
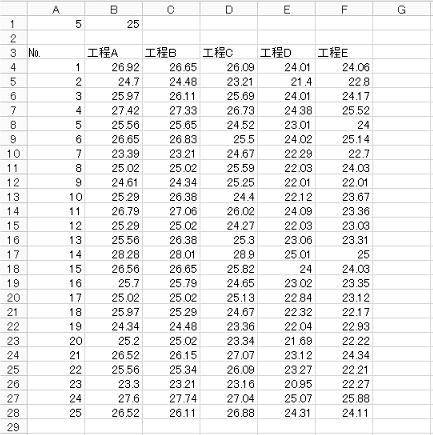
1)データファイルの作成
SA&RA ProXのデータファイルはEXCELか専用のエディターを用いて作成するが、以下の作成例はEXCELを用いて作成したものである。SA&RA
ProXがcsvデータとして読み込む際に、データ範囲を特定する為に入力エリアが決められている(詳細にはSA&RA ProXの頁を参照)だけで、基本入力操作はEXCELのそれである。
2)解析結果
SA&RA ProXでは分散分析表、母平均の推定、母平均の差の検定、母標準偏差の推定値が出力されるが、分散分析表の計算結果が上記計算結果と一致していることが分かる。

プログラムでは母平均の推定値のグラフが別ウィンドウで表示される。工程C→工程Dにおける変化が確認できる。
3.直交配列表実験
3.1因子水準表の作成
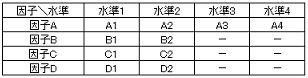
ある製品の特定環境における耐久性改善のため4因子(A,B,C,D)を取り上げ因子Aのみ4水準、他は2水準に設定することになった。過去の知見情報よりこれらの因子間の交互作用は確認されていないので、交互作用は取り上げないものとする。
3.2因子の割り付けと水準組み合わせ
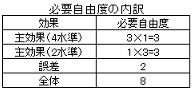
4水準因子が一つあるが他は全て2水準なので、基本的には2水準系直交配列表への割り付けになる。誤差項の自由度を2個確保し4水準因子は多水準法(必要な自由度は3)を適用すると、必要な自由度は以下表のように8個になる。このままではL8直交配列表(自由度7個)には割り付けられないためL16直交配列表(自由度15個)を適用することになるが、本試験が耐久性試験(ばらつきが大きくなることが予測される)であることを踏まえ、同一水準組み合わせ試料を各2個試験するものとした。繰り返しを入れることにより誤差の自由度を増やすことができるので、L8直交配列表に割り付けて実験することにした。多水準因子は主効果と交互作用の関係にある第1列~3列に割り付け、他の2水準因子はそのまま割り付けられるので以下表内の水準組み合わせ各2個により耐久性試験を実施した。
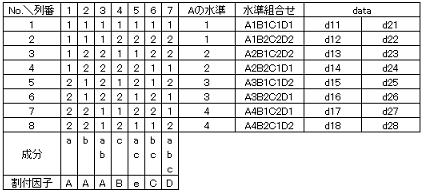
3.3解析データ
耐久性試験を実施した結果、以下のような故障時間線図が得られた。
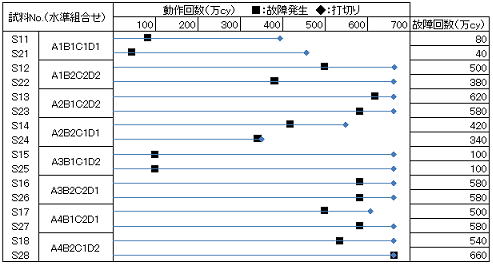
3.4分散分析表の作成
2水準系の各列の平方和の計算表から、各列の平方和は以下のように求まる。但し今回の実験では繰り返しを入れている関係から分母の値が8から16に変更されている。
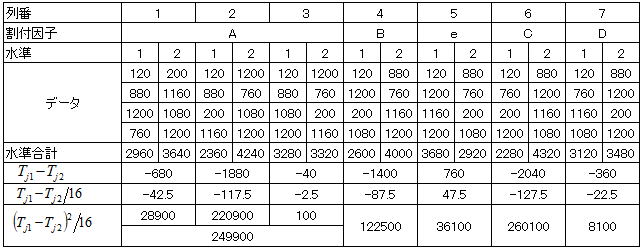
次に全データから全体平均を求め、全平方和を求めるとSt=699100が得られる。この値と上で計算した各列の平方和の合計が一致するかを確認してみよう。上の各列の平方和を計算すると676700となり以下の計算結果と一致しないが、これは繰り返しが入れてあるためである。誤差項は下の総平方和から上の誤差項を除く各列の平方和を差し引くと得られSe=699100-640600=58500となるが、この値も上の誤差項とは一致しない。繰り返しがある場合の誤差項は(不適合+純誤差)に分解でき、各列の平方和の計算における誤差項の割り付け列の合計(上の場合は1列のみ)が不適合成分となる。誤差項の自由度は全体の自由度15から各要因の自由度(3+1+1+1)を引いた値9となり、更に不適合成分の自由度は割り付け列の自由度になり以上を纏めると以下表のようになる。
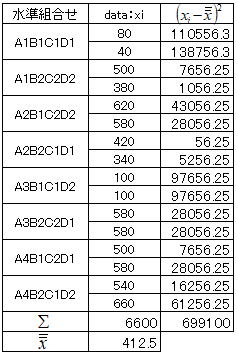
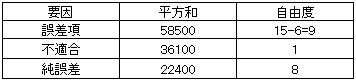
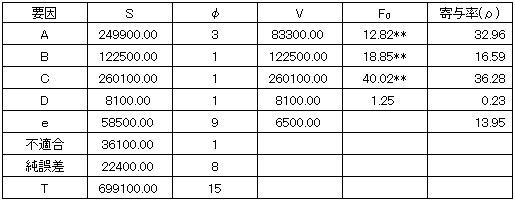
以上の計算結果及び寄与率(ρ%)を分散分析表に纏めると以下の分散分析表が得られる。要因A,B,Cが有意で分散比(F0)の順位はC→B→Aとなる。
3.5母平均の推定
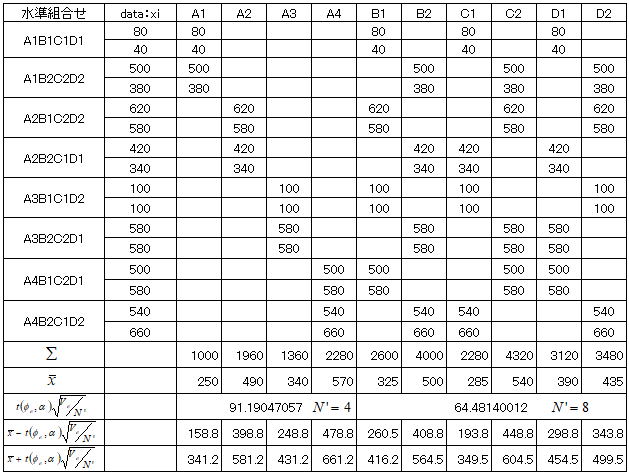
交互作用は取り上げていないので主効果の点推定値と信頼率(1-α)の信頼区間を求めると、以下表のように纏められる。信頼区間の推定式のN'は、多水準の因子AではN'=N/4=4他の因子はN'=N/2=8で計算することになる。
3.6耐久性改善手法と改善係数の推定
現在の標準仕様はA1B1C2D1なので先ずこの組み合わせにおける母平均を推定する。
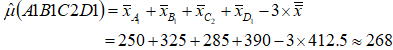
解析結果における最適水準はA4B2C2D2であるが、因子Dの有意差はないため設計上の選択肢により以下の組み合わせを取り上げた。
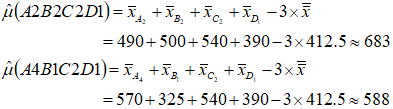
以上により現在の標準仕様に対して上記二つの改善仕様に設計変更することで、特定環境における耐久性が2.2~2.5倍程度改善される可能性があることが分かった。
3.7母標準偏差の推定
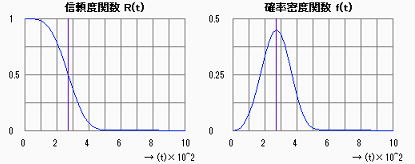
誤差分散から推定される母標準偏差の推定量は80.62(万cy)と推定された。この値は母平均の推定値との相対では非常に大きな値(ばらつきが非常に大きい)になるが、解析データが耐久性試験データであることを考慮すると特別に大きい値とは言えない。本題のような摩耗系故障における耐久性試験では、ワイブル形状Par.が5以下(時間領域のばらつき範囲が概ね5倍以上)の分布はいくらでもあり、標準仕様の故障分布(μ,σ)=(270,80)をワイブル分布と仮定してシミュレーションすると、下図に示すように形状Par.は概ねm=3.5前後と推定され摩耗系故障のばらつきとして特に大きいとは言えない。
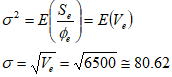
3.7プログラム(SA&RA ProX)による解析
1)データファイルの作成
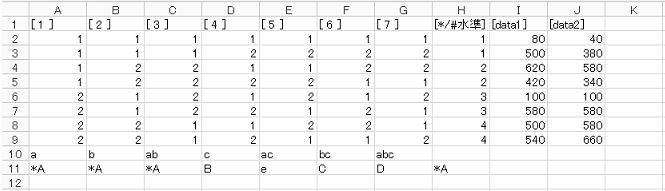
SA&RA ProXの直交配列表実験用データファイルは、実験計画に対応した直交配列表をベースに作成されたEXCELデータフォーマットを使用して作成する。以下は本題の作成例であるが、入力するのは割り付け因子(各列)、擬(多)水準の因子水準、解析データなどである。
2)解析結果
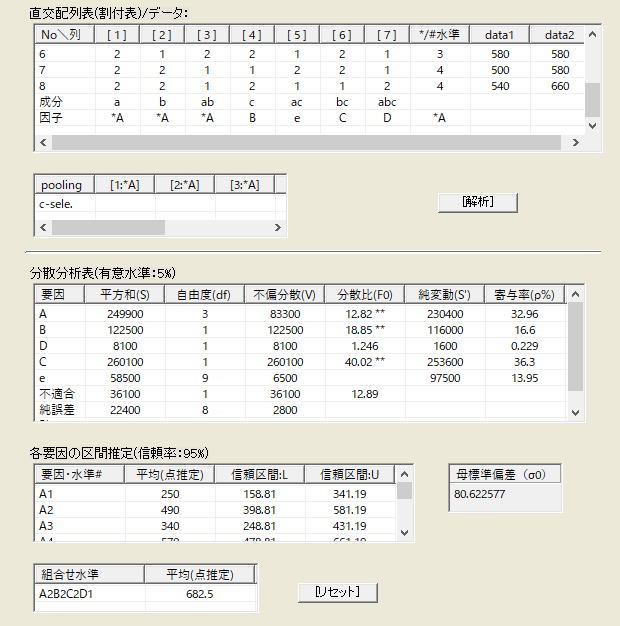
下図はSA&RA ProXの直交配列表実験の解析ウィンドウである。分散分析表、各要因の区間推定、任意組合せ水準の母平均の点推定値、母標準偏差の推定値などが出力される。なお本題ではプーリング処理はしないが、仮にプーリングする場合は中断のプーリング指定欄で指定した後で再度解析を実施することになる。分散分析表の各値及び各要因の区間推定値が、上の計算結果と一致していることが分かる。
下図は各要因の区間推定値のグラフ出力である。因子Aの母平均の推定値が交互作用があるかのような変化になっているが、因子Aの水準は物理量の水準変化ではないので問題はない。3.2項で示した改善手法の水準組み合わせ(A2B2C2D1及びA4B2C2D1)の妥当性が確認できる。
4.実践するためのポイント
4-1特性(Y)の決定
測定可能でかつ定量的な物理量であること、統計的に管理できる(正規分布である)ことが重要である。しかし例えば部品の摩耗量など、特性アイテムによっては必ずしも直接測定できない(特に実験継続中において)場合もある。このような場合は測定可能な代替え特性(それが起きることにより影響を受ける機能特性など)を検討し、適正な特性に置き換える必要がある。信頼性(耐久性)データの場合は全てのデータが正規分布になる確証はないが、摩耗系故障を扱う場合は正規分布に近似しているものとして扱う。
4.2要因(X)の選定方法
実験要因の選定にあたっては、次の二つの項目に分けて考えることが重要である。
1)実験担当者が任意にその中心値や水準を決定できる因子。寸法、形状、材質、電子部品の種類や定数(抵抗値など)などがある。
2)特性をばらつかせる因子。 環境条件、使用条件、製品(部品)間ばらつきなどが挙げられる。事前に関連する情報(文献や過去の技術資料、現在までの技術的知見、プロセスの現場など)を十分調査し、関係者の意見なども参考にした上で“上記の二つの観点から特性に影響があるかもしれない因子”をリストアップする。この際に“特性要因図”を作成することは有効な手法の一つになる。
リストアップされた因子からいずれを選定するかについては、影響度の大きさ(定性的な判断で可)、水準の維持管理が可能であるか、実験規模(コスト)などを考慮の上選定する。
4.3因子水準の設定
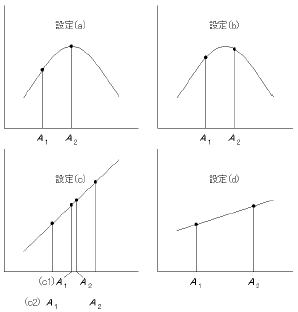
因子水準の設定において最も重要なポイントは、現在の設計仕様(若しくは状態など)をベンチマークとして比較できるよう各因子水準に設定することである。材料や処理方法などが2種類しかない場合を除き、計量的な因子では基本的には水準数を多く取った方がより良い条件(特性値を望ましい値に近付ける条件)を見付けることができる。しかしむやみに多水準にすることは実験回数の増大に繋がるため、原則として因子水準は2水準~4水準の範囲で設定すべきである。計量的な因子を2水準で設定する場合は、水準間隔の設定により有意になりやすい設定となりにくい場合があるので注意する必要がある。
4.4交互作用の取扱い
取り上げる交互作用は2要因交互作用のみとするが、2要因交互作用についてもその全てを取り上げようとすると実験回数の増大を招くので、技術的な見地から“考慮すべき交互作用”と“無視できる交互作用”を予め明確に区別し、必要な自由度のみを確保する。
4.5誤差(項)の自由度
分散分析を行うためには取り上げた各要因の効果情報と共に、誤差の情報(自由度)が少なくとも1個以上必要になる。この情報をどこから得るかについては、誤差も割り付け対象(要因)の一つとして考えると分かり易い。割り付けの段階では要因効果の自由度を確保したいことから誤差の自由度は少なく(1~2個)なりがちであるが、統計的観点(検定の検出力)からは誤差の自由度は大きい程良く、割り付け時における誤差の自由度は2個以上を推奨する。この観点から有意でない要因はプーリングが可能か検討し、可能であるならばプーリングして誤差項の自由度を大きくすべきである。
4.6実験計画法の普及効果
理論編でも述べてあるが、早く答えを得たいがための任意因子の組合わせ(実験回数の絞り込み)による実験は、特性(Y)に対し各因子(Xi)水準がどの程度影響(効果)しているかまでは判断できず、変化因子/水準の優劣はその組み合わせ条件でのみ言えるだけで、その場に限ればブレークスルーできる可能性は高いが別の製品で要素データとして活かせるかは全く別の話である。実験計画法を普及させるということは、以下における実験業務全般の技術力を高めることに繋がる。
1)特性(Y:従属変数)に対する要因(X:独立変数)の効果的な取り上げ。
2)実験回数の削減(目的に沿った効果的な組合せによる工数削減)技術。
3)実験結果の分析評価技術。
4)要因の影響度合いの定量化(分散分析による評価)。
5)有効活用できるデータ(設計要素データ)の蓄積。